歸并排序怎么排

.example-btn{color:#fff;background-color:#5cb85c;border-color:#4cae4c}.example-btn:hover{color:#fff;background-color:#47a447;border-color:#398439}.example-btn:active{background-image:none}div.example{width:98%;color:#000;background-color:#f6f4f0;background-color:#d0e69c;background-color:#dcecb5;background-color:#e5eecc;margin:0 0 5px 0;padding:5px;border:1px solid #d4d4d4;background-image:-webkit-linear-gradient(#fff,#e5eecc 100px);background-image:linear-gradient(#fff,#e5eecc 100px)}div.example_code{line-height:1.4em;width:98%;background-color:#fff;padding:5px;border:1px solid #d4d4d4;font-size:110%;font-family:Menlo,Monaco,Consolas,"Andale Mono","lucida console","Courier New",monospace;word-break:break-all;word-wrap:break-word}div.example_result{background-color:#fff;padding:4px;border:1px solid #d4d4d4;width:98%}div.code{width:98%;border:1px solid #d4d4d4;background-color:#f6f4f0;color:#444;padding:5px;margin:0}div.code div{font-size:110%}div.code div,div.code p,div.example_code p{font-family:"courier new"}pre{margin:15px auto;font:12px/20px Menlo,Monaco,Consolas,"Andale Mono","lucida console","Courier New",monospace;white-space:pre-wrap;word-break:break-all;word-wrap:break-word;border:1px solid #ddd;border-left-width:4px;padding:10px 15px}

排序算法是《數(shù)據(jù)結(jié)構(gòu)與算法》中最基本的算法之一。排序算法可以分為內(nèi)部排序和外部排序，內(nèi)部排序是數(shù)據(jù)記錄在內(nèi)存中進(jìn)行排序，而外部排序是因排序的數(shù)據(jù)很大，一次不能容納全部的排序記錄，在排序過(guò)程中需要訪問(wèn)外存。常見的內(nèi)部排序算法有：插入排序、希爾排序、選擇排序、冒泡排序、歸并排序、快速排序、堆排序、基數(shù)排序等。以下是歸并排序算法：

歸并排序（Merge sort）是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法（Divide and Conquer）的一個(gè)非常典型的應(yīng)用。

作為一種典型的分而治之思想的算法應(yīng)用，歸并排序的實(shí)現(xiàn)由兩種方法：

自上而下的遞歸（所有遞歸的方法都可以用迭代重寫，所以就有了第 2 種方法）；自下而上的迭代；

在《數(shù)據(jù)結(jié)構(gòu)與算法 JavaScript 描述》中，作者給出了自下而上的迭代方法。但是對(duì)于遞歸法，作者卻認(rèn)為：

However, it is not possible to do so in JavaScript, as the recursion goes too deep for the language to handle.

然而，在 JavaScript 中這種方式不太可行，因?yàn)檫@個(gè)算法的遞歸深度對(duì)它來(lái)講太深了。

說(shuō)實(shí)話，我不太理解這句話。意思是 JavaScript 編譯器內(nèi)存太小，遞歸太深容易造成內(nèi)存溢出嗎？還望有大神能夠指教。

和選擇排序一樣，歸并排序的性能不受輸入數(shù)據(jù)的影響，但表現(xiàn)比選擇排序好的多，因?yàn)槭冀K都是 O(nlogn) 的時(shí)間復(fù)雜度。代價(jià)是需要額外的內(nèi)存空間。

2. 算法步驟

申請(qǐng)空間，使其大小為兩個(gè)已經(jīng)排序序列之和，該空間用來(lái)存放合并后的序列；

設(shè)定兩個(gè)指針，最初位置分別為兩個(gè)已經(jīng)排序序列的起始位置；

比較兩個(gè)指針?biāo)赶虻脑兀x擇相對(duì)小的元素放入到合并空間，并移動(dòng)指針到下一位置；

重復(fù)步驟 3 直到某一指針達(dá)到序列尾；

將另一序列剩下的所有元素直接復(fù)制到合并序列尾。

3. 動(dòng)圖演示

代碼實(shí)現(xiàn)JavaScript實(shí)例 function mergeSort(arr) { ?// 采用自上而下的遞歸方法? ? var len = arr.length;? ? if(len < 2) {? ? ? ? return arr;? ? }? ? var middle = Math.floor(len / 2),? ? ? ? left = arr.slice(0, middle),? ? ? ? right = arr.slice(middle);? ? return merge(mergeSort(left), mergeSort(right));}function merge(left, right){? ? var result = [];? ? while (left.length && right.length) {? ? ? ? if (left[0] <= right[0]) {? ? ? ? ? ? result.push(left.shift());? ? ? ? } else {? ? ? ? ? ? result.push(right.shift());? ? ? ? }? ? }? ? while (left.length)? ? ? ? result.push(left.shift());? ? while (right.length)? ? ? ? result.push(right.shift());? ? return result;}Python實(shí)例 def mergeSort(arr):? ? import math? ? if(len(arr)<2):? ? ? ? return arr? ? middle = math.floor(len(arr)/2)? ? left, right = arr[0:middle], arr[middle:]? ? return merge(mergeSort(left), mergeSort(right))def merge(left,right):? ? result = []? ? while left and right:? ? ? ? if left[0] <= right[0]:? ? ? ? ? ? result.append(left.pop(0))? ? ? ? else:? ? ? ? ? ? result.append(right.pop(0));? ? while left:? ? ? ? result.append(left.pop(0))? ? while right:? ? ? ? result.append(right.pop(0));? ? return resultGo 實(shí)例 func mergeSort(arr []int) []int {? ? ? ? length := len(arr)? ? ? ? if length < 2 {? ? ? ? ? ? ? ? return arr? ? ? ? }? ? ? ? middle := length / 2? ? ? ? left := arr[0:middle]? ? ? ? right := arr[middle:]? ? ? ? return merge(mergeSort(left), mergeSort(right))}func merge(left []int, right []int) []int {? ? ? ? var result []int? ? ? ? for len(left) != 0 && len(right) != 0 {? ? ? ? ? ? ? ? if left[0] <= right[0] {? ? ? ? ? ? ? ? ? ? ? ? result = append(result, left[0])? ? ? ? ? ? ? ? ? ? ? ? left = left[1:]? ? ? ? ? ? ? ? } else {? ? ? ? ? ? ? ? ? ? ? ? result = append(result, right[0])? ? ? ? ? ? ? ? ? ? ? ? right = right[1:]? ? ? ? ? ? ? ? }? ? ? ? }? ? ? ? for len(left) != 0 {? ? ? ? ? ? ? ? result = append(result, left[0])? ? ? ? ? ? ? ? left = left[1:]? ? ? ? }? ? ? ? for len(right) != 0 {? ? ? ? ? ? ? ? result = append(result, right[0])? ? ? ? ? ? ? ? right = right[1:]? ? ? ? }? ? ? ? return result}Java實(shí)例 public class MergeSort implements IArraySort {? ? @Override? ? public int[] sort(int[] sourceArray) throws Exception {? ? ? ? // 對(duì) arr 進(jìn)行拷貝，不改變參數(shù)內(nèi)容? ? ? ? int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);? ? ? ? if (arr.length < 2) {? ? ? ? ? ? return arr;? ? ? ? }? ? ? ? int middle = (int) Math.floor(arr.length / 2);? ? ? ? int[] left = Arrays.copyOfRange(arr, 0, middle);? ? ? ? int[] right = Arrays.copyOfRange(arr, middle, arr.length);? ? ? ? return merge(sort(left), sort(right));? ? }? ? protected int[] merge(int[] left, int[] right) {? ? ? ? int[] result = new int[left.length + right.length];? ? ? ? int i = 0;? ? ? ? while (left.length > 0 && right.length > 0) {? ? ? ? ? ? if (left[0] <= right[0]) {? ? ? ? ? ? ? ? result[i++] = left[0];? ? ? ? ? ? ? ? left = Arrays.copyOfRange(left, 1, left.length);? ? ? ? ? ? } else {? ? ? ? ? ? ? ? result[i++] = right[0];? ? ? ? ? ? ? ? right = Arrays.copyOfRange(right, 1, right.length);? ? ? ? ? ? }? ? ? ? }? ? ? ? while (left.length > 0) {? ? ? ? ? ? result[i++] = left[0];? ? ? ? ? ? left = Arrays.copyOfRange(left, 1, left.length);? ? ? ? }? ? ? ? while (right.length > 0) {? ? ? ? ? ? result[i++] = right[0];? ? ? ? ? ? right = Arrays.copyOfRange(right, 1, right.length);? ? ? ? }? ? ? ? return result;? ? }}PHP實(shí)例 function mergeSort($arr){? ? $len = count($arr);? ? if ($len < 2) {? ? ? ? return $arr;? ? }? ? $middle = floor($len / 2);? ? $left = array_slice($arr, 0, $middle);? ? $right = array_slice($arr, $middle);? ? return merge(mergeSort($left), mergeSort($right));}function merge($left, $right){? ? $result = [];? ? while (count($left) > 0 && count($right) > 0) {? ? ? ? if ($left[0] <= $right[0]) {? ? ? ? ? ? $result[] = array_shift($left);? ? ? ? } else {? ? ? ? ? ? $result[] = array_shift($right);? ? ? ? }? ? }? ? while (count($left))? ? ? ? $result[] = array_shift($left);? ? while (count($right))? ? ? ? $result[] = array_shift($right);? ? return $result;}C實(shí)例 int min(int x, int y) {? ? return x < y ? x : y;}void merge_sort(int arr[], int len) {? ? int *a = arr;? ? int *b = (int *) malloc(len * sizeof(int));? ? int seg, start;? ? for (seg = 1; seg < len; seg += seg) {? ? ? ? for (start = 0; start < len; start += seg * 2) {? ? ? ? ? ? int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);? ? ? ? ? ? int k = low;? ? ? ? ? ? int start1 = low, end1 = mid;? ? ? ? ? ? int start2 = mid, end2 = high;? ? ? ? ? ? while (start1 < end1 && start2 < end2)? ? ? ? ? ? ? ? b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];? ? ? ? ? ? while (start1 < end1)? ? ? ? ? ? ? ? b[k++] = a[start1++];? ? ? ? ? ? while (start2 < end2)? ? ? ? ? ? ? ? b[k++] = a[start2++];? ? ? ? }? ? ? ? int *temp = a;? ? ? ? a = b;? ? ? ? b = temp;? ? }? ? if (a != arr) {? ? ? ? int i;? ? ? ? for (i = 0; i < len; i++)? ? ? ? ? ? b[i] = a[i];? ? ? ? b = a;? ? }? ? free(b);}

遞歸版：

實(shí)例 void merge_sort_recursive(int arr[], int reg[], int start, int end) {? ? if (start >= end)? ? ? ? return;? ? int len = end - start, mid = (len >> 1) + start;? ? int start1 = start, end1 = mid;? ? int start2 = mid + 1, end2 = end;? ? merge_sort_recursive(arr, reg, start1, end1);? ? merge_sort_recursive(arr, reg, start2, end2);? ? int k = start;? ? while (start1 <= end1 && start2 <= end2)? ? ? ? reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];? ? while (start1 <= end1)? ? ? ? reg[k++] = arr[start1++];? ? while (start2 <= end2)? ? ? ? reg[k++] = arr[start2++];? ? for (k = start; k <= end; k++)? ? ? ? arr[k] = reg[k];}void merge_sort(int arr[], const int len) {? ? int reg[len];? ? merge_sort_recursive(arr, reg, 0, len - 1);}C++

迭代版：

實(shí)例 template // 整數(shù)或浮點(diǎn)數(shù)皆可使用,若要使用物件(class)時(shí)必須設(shè)定"小於"(<)的運(yùn)算子功能void merge_sort(T arr[], int len) {? ? T *a = arr;? ? T *b = new T[len];? ? for (int seg = 1; seg < len; seg += seg) {? ? ? ? for (int start = 0; start < len; start += seg + seg) {? ? ? ? ? ? int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);? ? ? ? ? ? int k = low;? ? ? ? ? ? int start1 = low, end1 = mid;? ? ? ? ? ? int start2 = mid, end2 = high;? ? ? ? ? ? while (start1 < end1 && start2 < end2)? ? ? ? ? ? ? ? b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];? ? ? ? ? ? while (start1 < end1)? ? ? ? ? ? ? ? b[k++] = a[start1++];? ? ? ? ? ? while (start2 < end2)? ? ? ? ? ? ? ? b[k++] = a[start2++];? ? ? ? }? ? ? ? T *temp = a;? ? ? ? a = b;? ? ? ? b = temp;? ? }? ? if (a != arr) {? ? ? ? for (int i = 0; i < len; i++)? ? ? ? ? ? b[i] = a[i];? ? ? ? b = a;? ? }? ? delete[] b;}

遞歸版：

實(shí)例 void Merge(vector &Array, int front, int mid, int end) {? ? // preconditions:? ? // Array[front...mid] is sorted? ? // Array[mid+1 ... end] is sorted? ? // Copy Array[front ... mid] to LeftSubArray? ? // Copy Array[mid+1 ... end] to RightSubArray? ? vector LeftSubArray(Array.begin() + front, Array.begin() + mid + 1);? ? vector RightSubArray(Array.begin() + mid + 1, Array.begin() + end + 1);? ? int idxLeft = 0, idxRight = 0;? ? LeftSubArray.insert(LeftSubArray.end(), numeric_limits::max());? ? RightSubArray.insert(RightSubArray.end(), numeric_limits::max());? ? // Pick min of LeftSubArray[idxLeft] and RightSubArray[idxRight], and put into Array[i]? ? for (int i = front; i <= end; i++) {? ? ? ? if (LeftSubArray[idxLeft] < RightSubArray[idxRight]) {? ? ? ? ? ? Array[i] = LeftSubArray[idxLeft];? ? ? ? ? ? idxLeft++;? ? ? ? } else {? ? ? ? ? ? Array[i] = RightSubArray[idxRight];? ? ? ? ? ? idxRight++;? ? ? ? }? ? }}void MergeSort(vector &Array, int front, int end) {? ? if (front >= end)? ? ? ? return;? ? int mid = (front + end) / 2;? ? MergeSort(Array, front, mid);? ? MergeSort(Array, mid + 1, end);? ? Merge(Array, front, mid, end);}C#實(shí)例 public static List sort(List lst) {? ? if (lst.Count <= 1)? ? ? ? return lst;? ? int mid = lst.Count / 2;? ? List left = new List(); ?// 定義左側(cè)List? ? List right = new List(); // 定義右側(cè)List? ? // 以下兩個(gè)循環(huán)把 lst 分為左右兩個(gè) List? ? for (int i = 0; i < mid; i++)? ? ? ? left.Add(lst[i]);? ? for (int j = mid; j < lst.Count; j++)? ? ? ? right.Add(lst[j]);? ? left = sort(left);? ? right = sort(right);? ? return merge(left, right);}///

/// 合併兩個(gè)已經(jīng)排好序的List///

/// 左側(cè)List/// 右側(cè)List/// static List merge(List left, List right) {? ? List temp = new List();? ? while (left.Count > 0 && right.Count > 0) {? ? ? ? if (left[0] <= right[0]) {? ? ? ? ? ? temp.Add(left[0]);? ? ? ? ? ? left.RemoveAt(0);? ? ? ? } else {? ? ? ? ? ? temp.Add(right[0]);? ? ? ? ? ? right.RemoveAt(0);? ? ? ? }? ? }? ? if (left.Count > 0) {? ? ? ? for (int i = 0; i < left.Count; i++)? ? ? ? ? ? temp.Add(left[i]);? ? }? ? if (right.Count > 0) {? ? ? ? for (int i = 0; i < right.Count; i++)? ? ? ? ? ? temp.Add(right[i]);? ? }? ? return temp;}Ruby實(shí)例 def merge list? return list if list.size < 2? pivot = list.size / 2? # Merge? lambda { |left, right|? ? final = []? ? until left.empty? or right.empty?? ? ? final << if left.first < right.first; left.shift else right.shift end? ? end? ? final + left + right? }.call merge(list[0...pivot]), merge(list[pivot..-1])end

參考地址：

https://github.com/hustcc/JS-Sorting-Algorithm/blob/master/5.mergeSort.md

https://zh.wikipedia.org/wiki/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F

以下是熱心網(wǎng)友對(duì)歸并排序算法的補(bǔ)充，僅供參考：

熱心網(wǎng)友提供的補(bǔ)充1：

分而治之

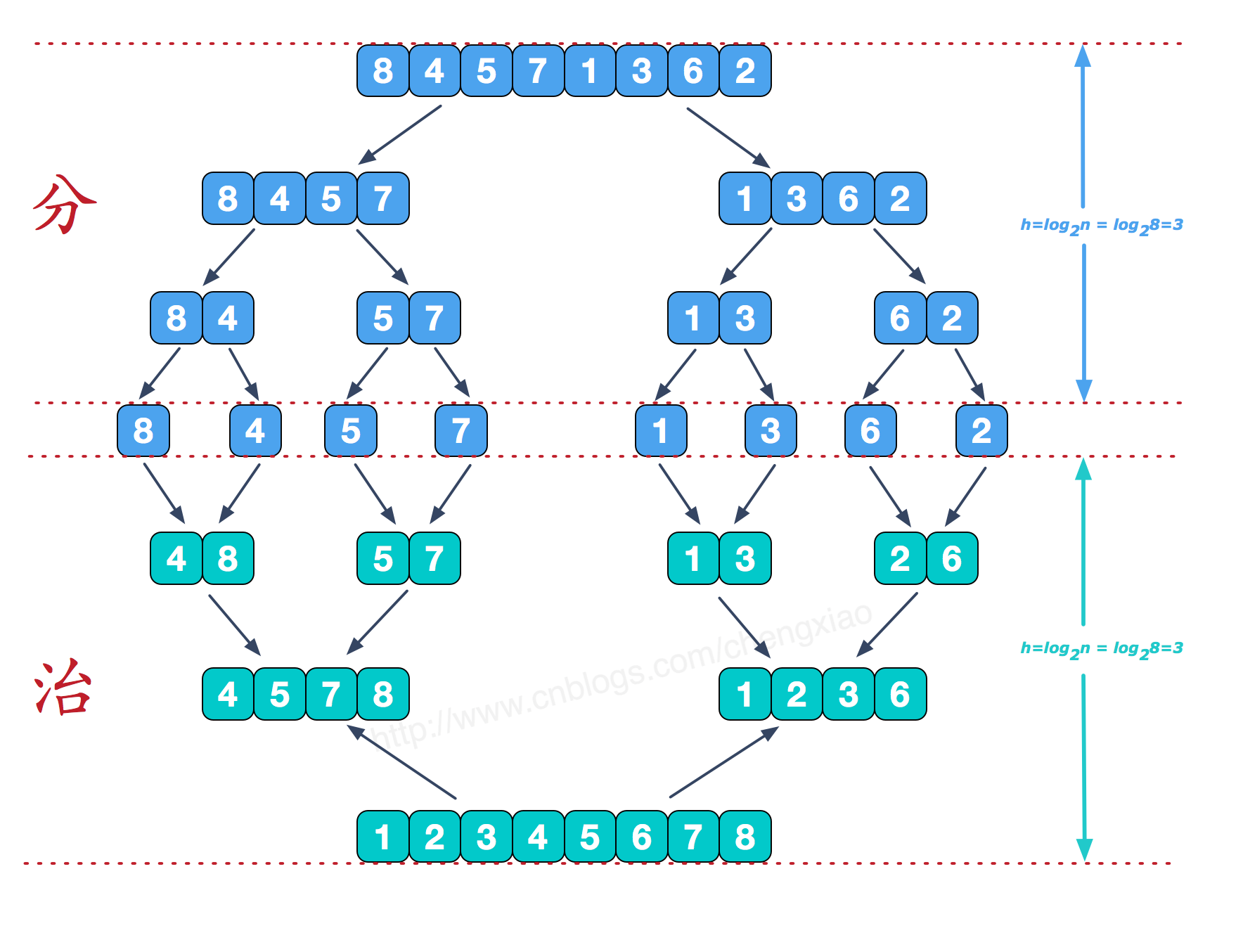
可以看到這種結(jié)構(gòu)很像一棵完全二叉樹，本文的歸并排序我們采用遞歸去實(shí)現(xiàn)（也可采用迭代的方式去實(shí)現(xiàn)）。分階段可以理解為就是遞歸拆分子序列的過(guò)程，遞歸深度為log2n。

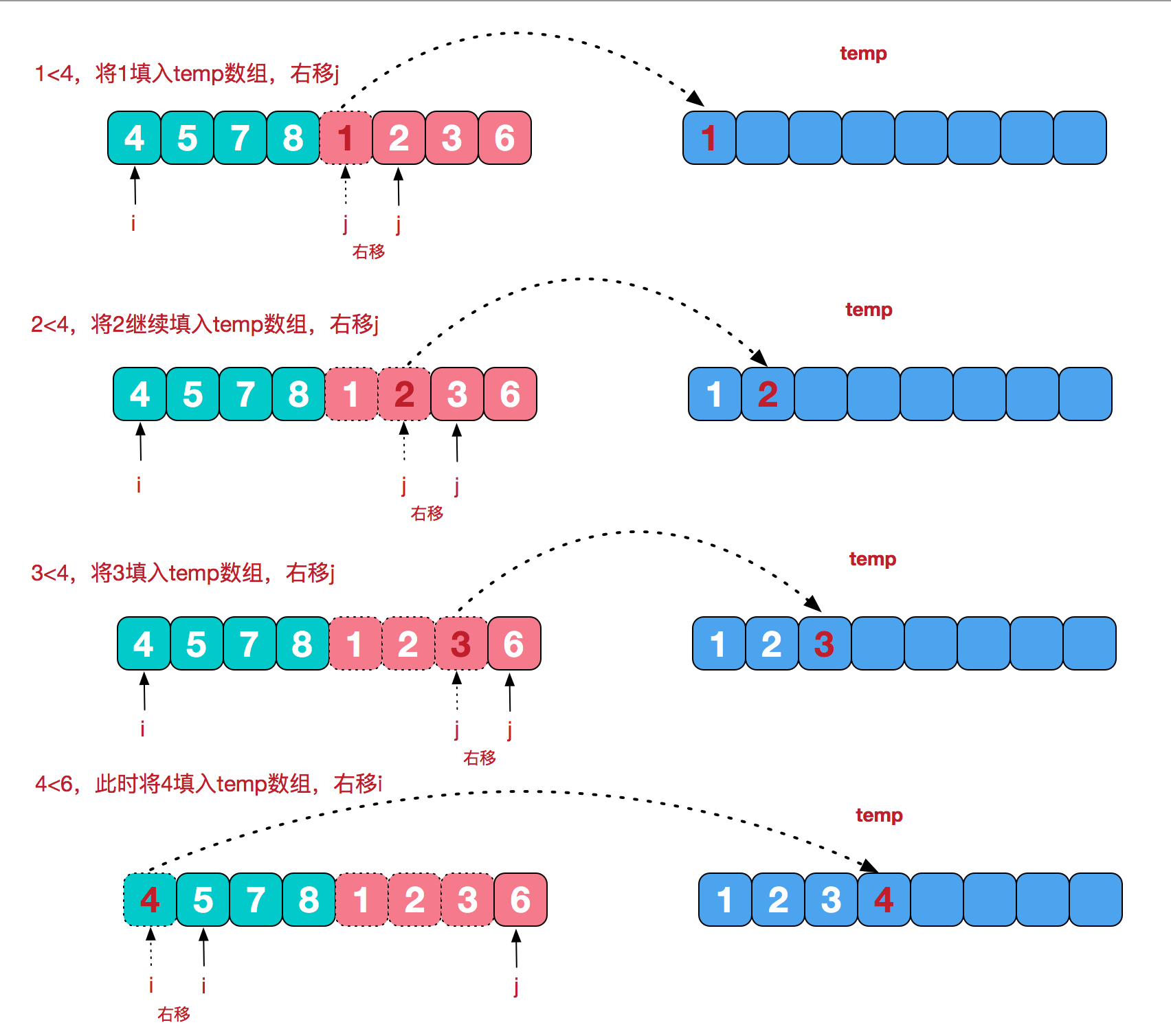
合并相鄰有序子序列

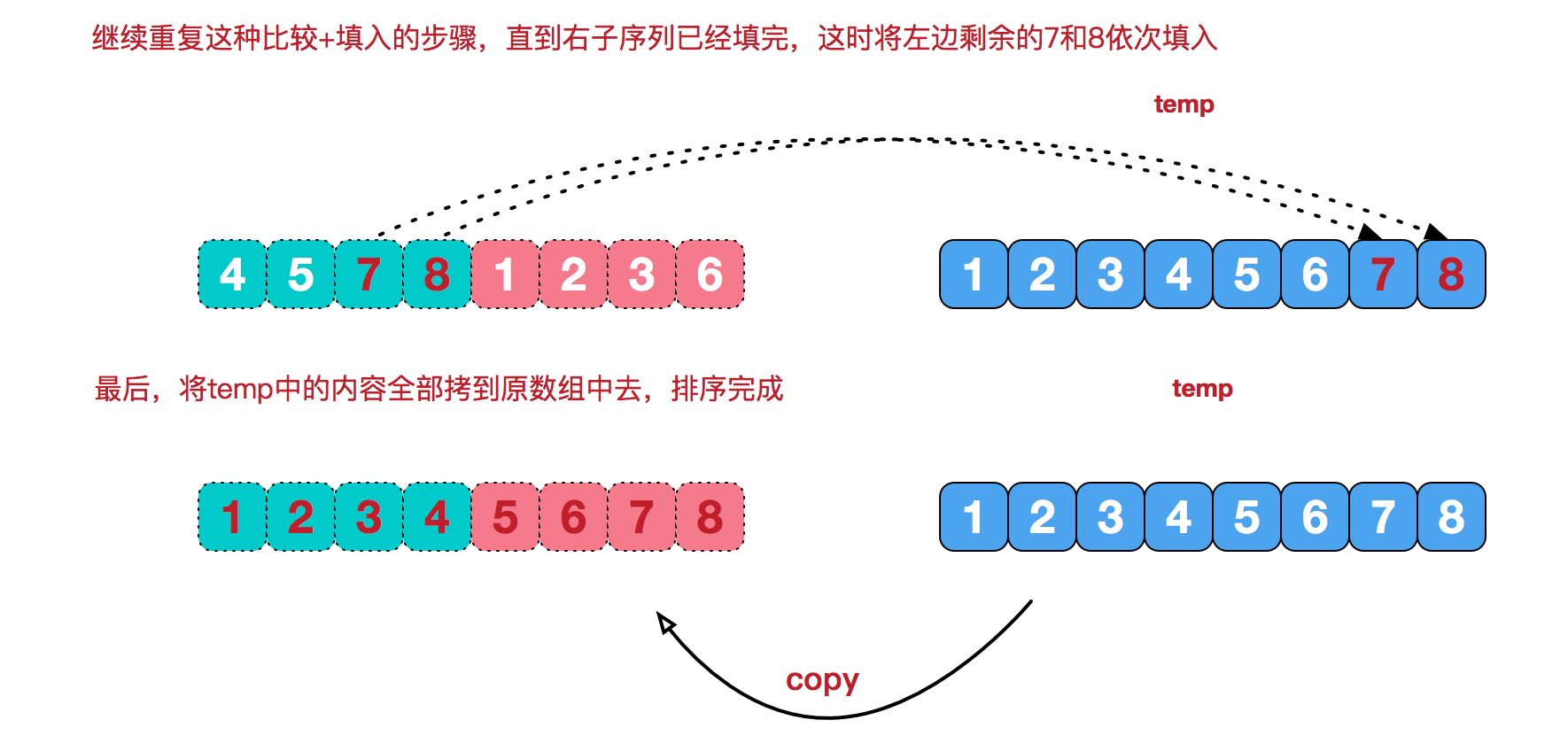
再來(lái)看看治階段，我們需要將兩個(gè)已經(jīng)有序的子序列合并成一個(gè)有序序列，比如上圖中的最后一次合并，要將[4,5,7,8]和[1,2,3,6]兩個(gè)已經(jīng)有序的子序列，合并為最終序列[1,2,3,4,5,6,7,8]，來(lái)看下實(shí)現(xiàn)步驟。

import java.util.Arrays;

/**
 * Created by chengxiao on 2016/12/8.
 */
public class MergeSort {
    public static void main(String []args){
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一個(gè)長(zhǎng)度等于原數(shù)組長(zhǎng)度的臨時(shí)數(shù)組，避免遞歸中頻繁開辟空間
        sort(arr,0,arr.length-1,temp);
    }
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left以上為歸并排序算法詳細(xì)介紹，插入排序、希爾排序、選擇排序、冒泡排序、歸并排序、快速排序、堆排序、基數(shù)排序等排序算法各有優(yōu)缺點(diǎn)，用一張圖概括： 
關(guān)于時(shí)間復(fù)雜度
平方階 (O(n2)) 排序 各類簡(jiǎn)單排序：直接插入、直接選擇和冒泡排序。
線性對(duì)數(shù)階 (O(nlog2n)) 排序 快速排序、堆排序和歸并排序；
O(n1+§)) 排序，§ 是介于 0 和 1 之間的常數(shù)。 希爾排序
線性階 (O(n)) 排序 基數(shù)排序，此外還有桶、箱排序。
關(guān)于穩(wěn)定性
穩(wěn)定的排序算法：冒泡排序、插入排序、歸并排序和基數(shù)排序。
不是穩(wěn)定的排序算法：選擇排序、快速排序、希爾排序、堆排序。
名詞解釋：
n：數(shù)據(jù)規(guī)模
k："桶"的個(gè)數(shù)
In-place：占用常數(shù)內(nèi)存，不占用額外內(nèi)存
Out-place：占用額外內(nèi)存
穩(wěn)定性：排序后 2 個(gè)相等鍵值的順序和排序之前它們的順序相同